Cepstrum

Molto ad alto livello si può dire che il Cepstrum non è nient'altro che lo Spectrum
di uno Spectrum. Ovvero che dopo essere passati dal time domain tramite la Trasformata di Fourier allo Spectrum, applichiamo una funzione logaritmica (tra poco vedremo perché) e infine l'Inverse Fourier Transform.

Visualizzare il Cepstrum

Abbiamo inizialmente un time-domain di un segnale audio, applicando la Trasformata di Fourier abbiamo poi il frequency domain.

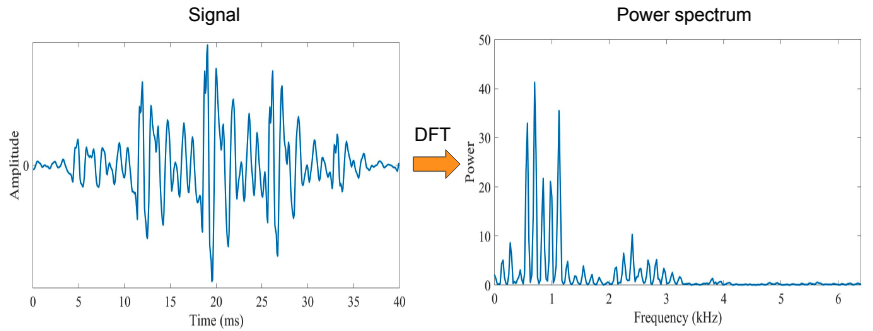
A questo punto applichiamo la funzione logaritmica, che semplice trasforma l'amplitudine in decibel.

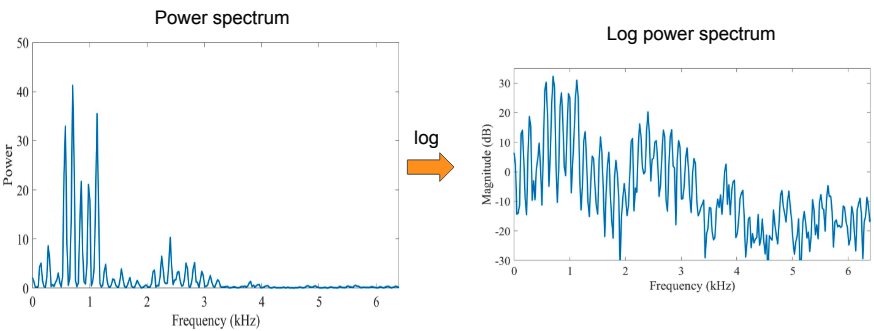
Nella funzione logaritmica dello spectrum, abbiamo un segnale continua che ha una struttura periodica. Quello che possiamo fare è usare questo spectrum tramite Trasformata di Fourier per vedere dove assume importanza la frequenza. Ma cosa abbiamo sull'asse delle x ? questa viene chiamata Quefrency e si calcola in ms. Dove abbiamo i picchi, come in questo caso rappresenta quanto presente questo quefrency è nel log spectrum di prima.

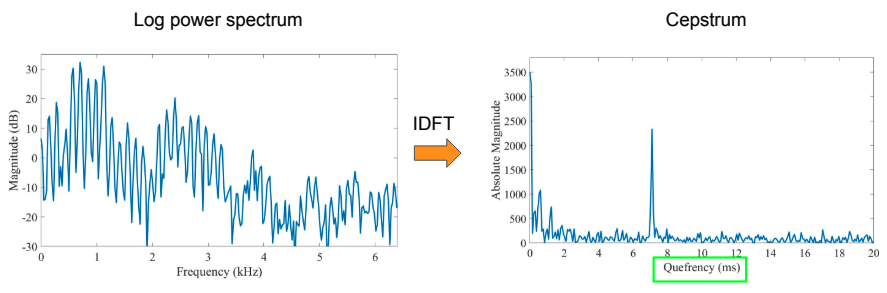
Ora per continuare occorre fare una piccola digressione sul tratto vocale.

Tratto vocale

Il tratto vocale è un sistema molto complesso che ha più elementi come la lingua, i denti, la gola e la cavità nasale. L'idea è che il modo in cui modelliamo il nostro tratto vocale andrà a produrre suoni diversi. Se pensiamo a questo come un suono digitale, possiamo vedere il tratto vocale come un filtro.

Generazione del discorso

Parte tutto dall'impulso glottale, ed è un segnale che fa rumore, poi passando dal tratto vocale viene modellato per creare il discorso.

Ora per comprendere a cosa è servito tutto questo torniamo al cepstrum di prima.

Capire il Cepstrum

Ora facciamo finta di avere la funzione logaritmica dello spectrum del discorso. Ora se estraiamo la spectral envelope di questa funzione osserviamo una cosa molto interessante, perché ci mostra informazioni sul timbro tramite i picchi, e questo feature vogliamo isolarla per fare speech recognition. La scoperta determinante qua, è che questa funzione risulta essere molto importante per la frequenza del tratto vocale.

Se ora a questa versione più riassuntiva della funzione sottraiamo quella originale, ricaviamo la terza figura presente nell'immagine. Ci rimane una funzione che cambia molto in fretta e possiamo chiamare questi i dettagli spettrali, ed è incredibili come questi dettagli mostrano molto bene la frequenza dell'impulso glottale.

Quindi possiamo concludere affermando che il discorso è come la convoluzione del tratto vocale e dell'impulso glottale.

Ma qual'è la matematica che sta dietro a tutto questo ?

Dove $x(t)$ è il nostro segnale originale, e poi abbiamo dall'altra parte dell'uguaglianza la convoluzione del tratto vocale $h(t)$ e dell'impulso glottale $e(t)$, e siamo nel time domain. Ma se ci muoviamo nel frequency domain e applichiamo la Trasformata di Fourier:

Avremo che lo spectrum del segnale è uguale ai due spectrum del tratto vocale e dell'impulso glottale moltiplicati. Ora applichiamo l'algoritmo all'uguaglianza:

ora se approfittiamo delle proprietà dell'algoritmo possiamo riscrivere questa formula così:

Il vantaggio di fare questo è che possiamo trattare i componenti in maniera separata. Ora possiamo fare delle operazioni molto interessanti, ad esempio visto che non siamo interessati all'impulso glottale per il processo, possiamo eliminarlo.

Ora dobbiamo trovare un processo tramite il quale partiamo da audio per poi isolare i componenti che non ci interessano.

Per partire facendo la Trasformata inversa di Fourier passiamo alla quefrency. Quindi ancora una volta prendiamo delle funzioni sinusoidali e cerchiamo di approssimare l'andamento delle frequenze, e questa operazione ha lo scopo in questo caso di decomporre nelle quefrency.

Nel nostro possiamo vedere dai grafici che abbiamo 4 picchi, quindi probabilmente un'onda sinusoidale che ha una frequenza di 4 hertz farà un buon lavoro di approssimazione.

Quindi quando ci muoveremo nel quefrency domain avremo un valore alto corrispettivo alla frequenza 4. Man mano che muoviamo sull'asse delle x aumentando la frequenza entreremo nei dettagli spettrali. Trovando ad esempio 100 hertz.

Quindi il punto principale è che avremo una separazione naturale e fisica delle informazioni sul segnale audio. Quindi con un'operazione poi chiamata "liftering"
che rimuove i componenti che non ci interessano.

Nella pratica però per estrarre i coefficienti cepstrals si usa la Discrete Cosine Transform, che è simile alla Trasformata inversa di Fourier ma con dei vantaggi.

Discrete Cosine Transform

Si tratta di una versione semplificata della Trasformata inversa di Fourier e ritorna i coefficienti come valori reali. Torna un numero di coefficienti che sono quelli in cui siamo interessati noi.

La Trasformata inversa di Fourier ritorna numeri complessi.

L'idea qui è che abbiamo dei coseni a differenze frequenze e cerchiamo di "fittarli" allo spectrum logaritmico. Ogni coseno avrà una frequenza diversa, e come risultato avrà un valore e questo valore sarà quanto bene quel coseno con quella specifica frequenza approssima al meglio lo spectrum logaritmico e quel valore è un mfcc. Maggiore è la velocità del coseno maggiore è il valore del coefficiente.

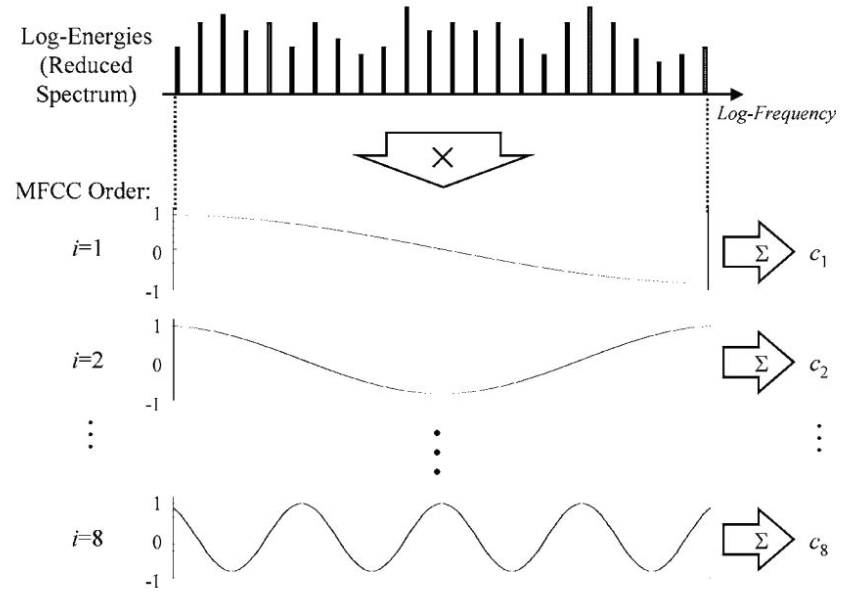
Coefficienti

I primi coefficienti sono quelli che mantengono la maggior parte dell'informazione. Se si vogliono visualizzare, sarà molto simile allo spectogram, questo perché possiamo pensarli come una matrice, sull'asse delle y abbiamo i diversi coefficienti e sulle colonne abbiamo i frames, quindi a ogni cella abbiamo il valore di un determinato valore di un coefficiente per il frame.