Come funziona la Trasformata di Fourier ?

Prima di tutto pensiamo a un suono come una composizione di note, ovvero più note sono messe insieme per dare l'output. Se pensiamo alle note singolarmente ed in maniera visiva sembreranno molto delle funzioni sinusoidali a diverse velocità.

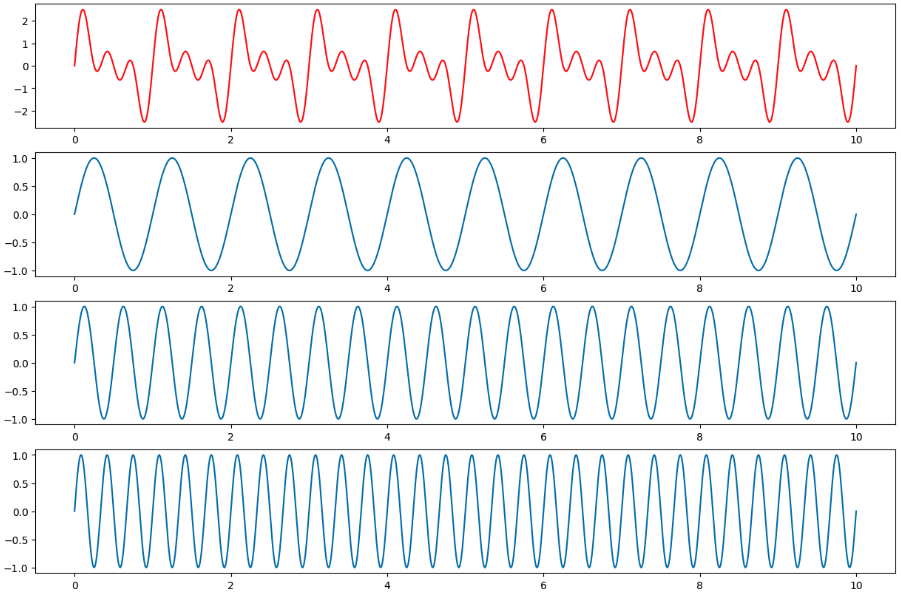
Ora il suono è ancora molto più complicato questo con moltissime altre varianti. Nel nostro processo di Mobile Recognition un microfono registra il suono come giù la somma di tutte queste componenti.

L'idea alla base è quella di creare un "macchina matematica", che tratta segnali in maniera dipendente dalle loro frequenze.

Partiamo da un esempio in cui abbiamo un segnale puro che ha solo $3beats/second$ e facciamo finta di osservare la porzione di segnale che va fino a $4,5seconds$.

L'idea geometrica è quello di prendere questo grafico e arrotolarlo intorno a un cerchio. Poi immaginiamo un vettore rotante che percorre questo segnale attorno all'origine. In più ogni punto nel tempo corrisponde in lunghezza all'altezza del grafo in quel momento, quindi punti alti nel grafo corrispondono a punti distanti dall'origine nel cerchio.

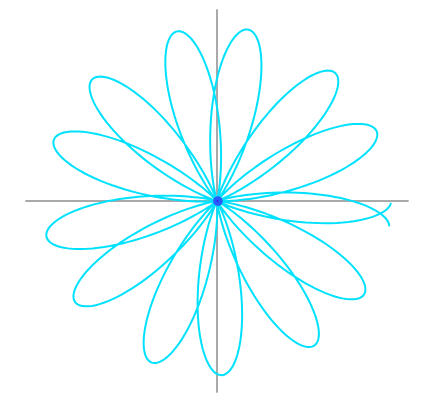
Ora immaginate di disegnarlo, in modo che 2 secondi nel grafo corrispondono a una singola rotazione nel cerchio. Quindi il nostro grafo gira alla velocità di mezzo cerchio al secondo. Ora è importante comprendere che abbiamo due frequenze, la prima che è quella del grafo di $3beats/second$ e la seconda che abbiamo scelto noi di $0.5cycles/second$, la velocità di questa seconda la decidiamo noi e possiamo renderla più veloce o lenta. Quest'ultima componente della velocità non è molto intuitiva, invece lo è il fatto che stiamo arrotolando il grafo attorno ad un cerchio.

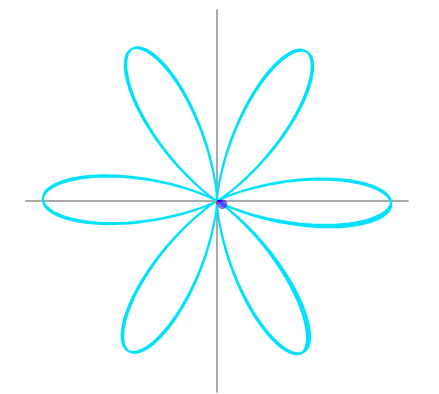
Ora un fatto molto particolare accade se la frequenza di rotazione e quella del segnale corrispondono, $3beats/second$. Tutti i punti alti del grafo appariranno nella parte destra del grafo.

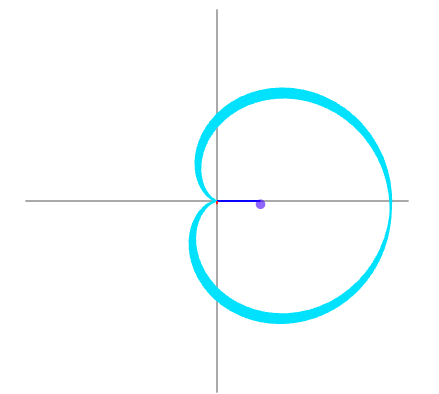
Ora se la domanda è: come possiamo usarla questa cosa ? avete perfettamente ragione, e sarà spiegato a breve.

Per quanto possa essere molta astratta come spiegazione cercate di seguirla. Immaginate che al centro del cerchio ci sia un centro di massa che è il grafo che si arrotola. Quindi praticamente il centro cambiamo posizione in base alla velocità del grafo sul cerchio, e risulterà quasi sempre essere al centro vicino all'origine.

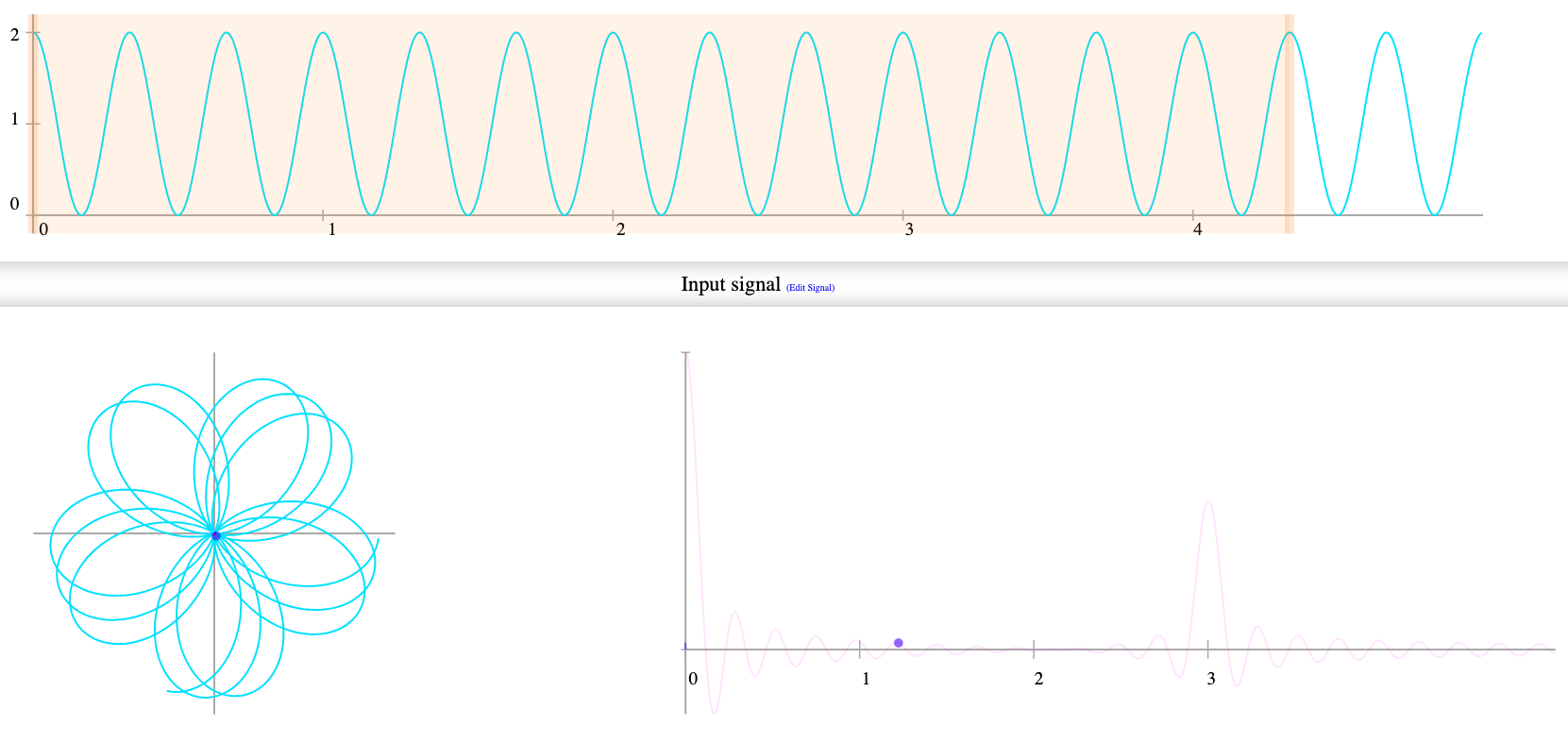
Ma se la frequenza del grafo e del cerchio sono la stessa, abbiamo detto sarà tutto sulla destra quindi il centro sarà a spostato anch'esso a destra, circa a metà dall'origine($0.5$). Beh questo vuol dire che la frequenza rappresentata frequency domain rappresenta proprio questo, ovvero ci sarà un picco quando sarà a $3$.

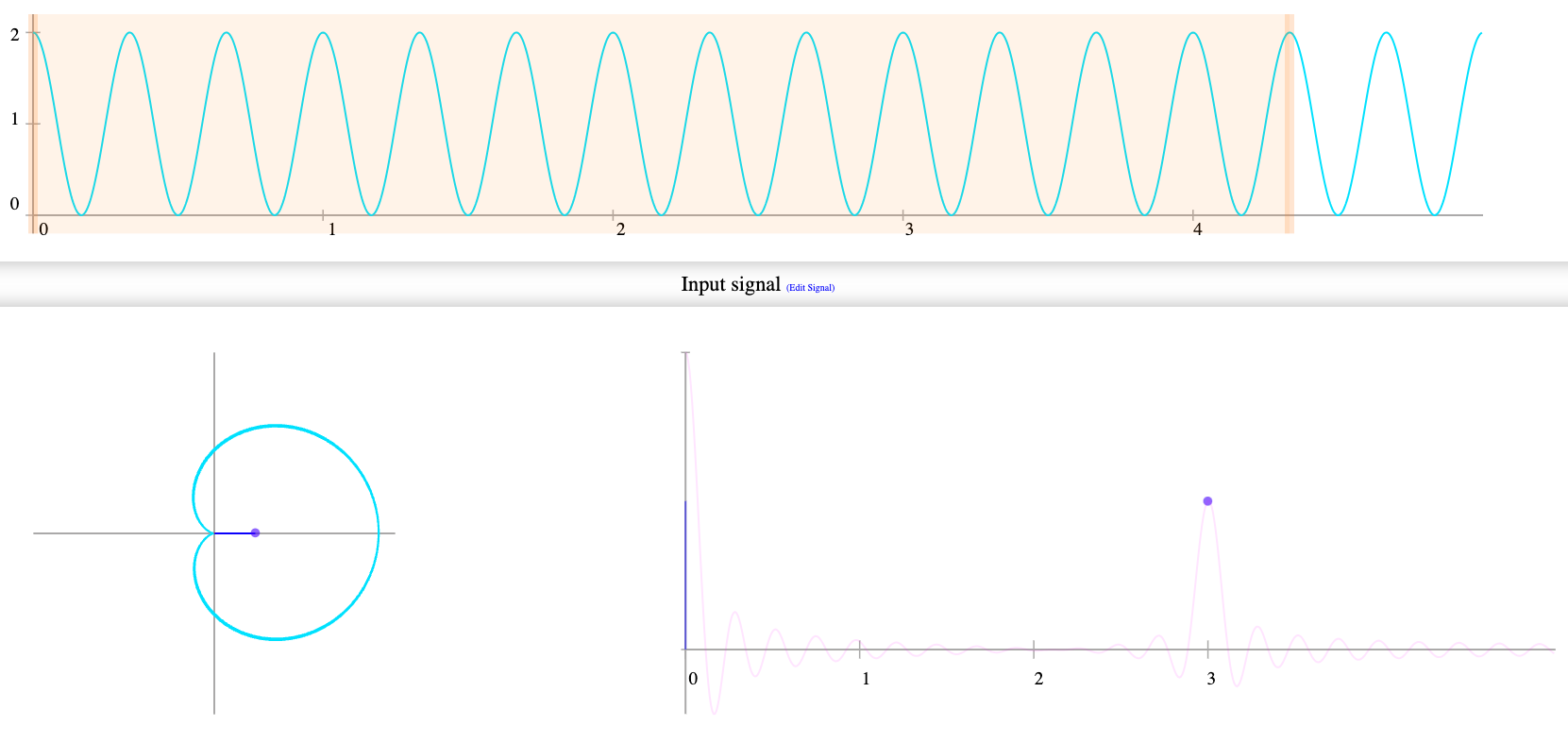
Ora arriva il punto forte di questa funzione, ovvero come possiamo tirare fuori più frequenze da un suono complesso. Semplicemente se sommiamo le frequenze per comporre un suono e poi lo arrotoliamo avremo di nuovo gli stessi picchi.

La trasformata di Fourier

L'intuizione è quella di decomporre il suono nei suoi diversi componenti delle frequenze.
Infatti, la trasformata di Fourier è in grado di convertire il suono dal time domain nel frequency domain

Cosa accade più precisamente

La prima cosa che accade applicando la trasformata di Fourier è quella di comparare il segnale originale con un gruppo di sinusoidi con le stesse frequenze. Abbiamo quindi un il segnale originale e un gruppo di onde sinusoidali che avranno frequenze diverse. Tramite questa comparazione si ottiene una magnitudine e una fase. La magnitudine indica quanto sono simili il segnale originale e la sinusoide, maggiore è la magnitudine maggiore è la somiglianza.

Passo per passo

Per dare una chiara e corretta spiegazione trasformata di Fourier, vi mostrerò passo per passo i vari procedimenti mostrando le varie rappresentazioni grafiche.

• Il primo passaggio da effettuare è quello di visualizzare il nostro audio tramite un waveform con sugli assi il tempo e l'amplitudine, quindi ci troviamo all'interno di un time domain.

  

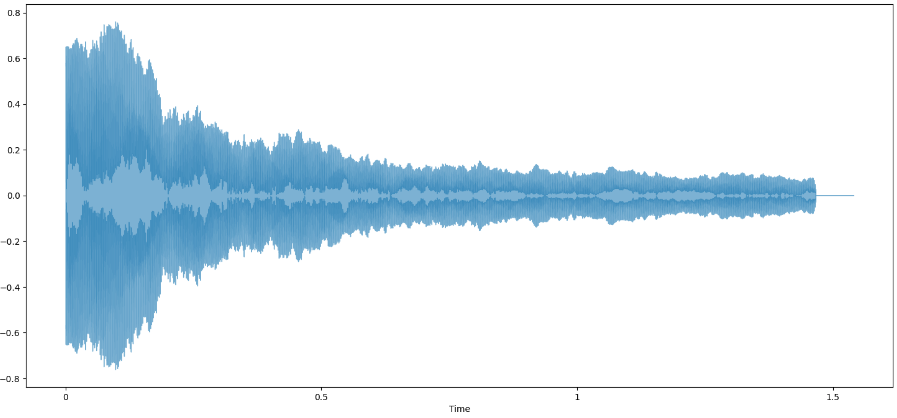
• Ora vogliamo, anticipiamo con lo spectrum quello che fa la Fast Fourier Transform solo per vedere i picchi di magnitudine. Quindi deriviamo lo spectrum tramite la Fast Fourier Transform e passiamo a una rappresentazione frequency domain.

  

• Ora ritornando al waveform, facciamo un po' di calcoli, calcoliamo prima di tutto la lunghezza del segnale, nel nostro caso facciamo finta sia di circa $34000$ samples. E la durata di ogni sample che si calcola l'inversa della sampling rate è di un valore molto piccolo alla potenza di $e^{-}5$. Ora calcoliamo ogni quanti secondi abbiamo un ciclo, e per farlo facciamo l'inversa del numero che rappresenta la differenza di frequenza tra i vari picchi di magnitudine, otteniamo circa $2ms$.

• Ora aumentiamo la risoluzione all'interno del waveform prendendo in considerazione solo $400$ samples, che ci danno circa $0.02s$ il che ci permetterà di vedere circa 10 cicli. Dunque prendendo solo $400$ samples abbiamo questa rappresentazione: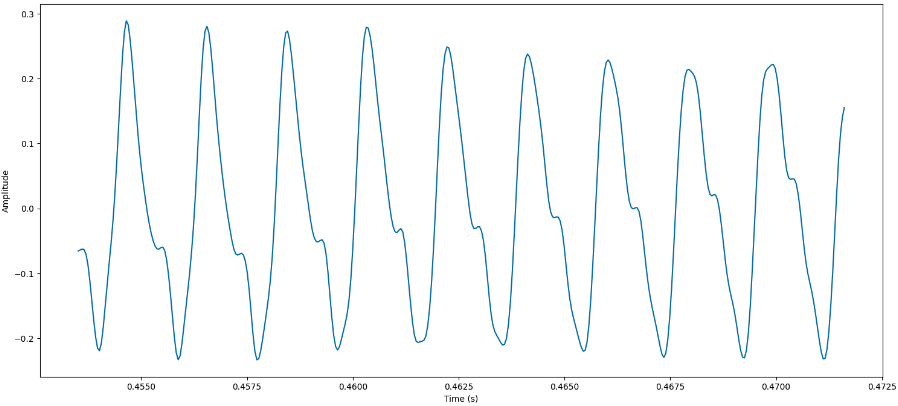

  

• Ora quello che vogliamo fare è comparare questo segnale con differenti sinusoidi a diverse frequenze. Facciamo una cosa molto semplice, prendiamo la formula della wave sine: $sin(2pi\ast (ft-phi))$
  Dove $ft$ è la frequenza e $phi$ è la fase. Ora mostrerò una rappresentazione con due sinusoidi a diverse fasi: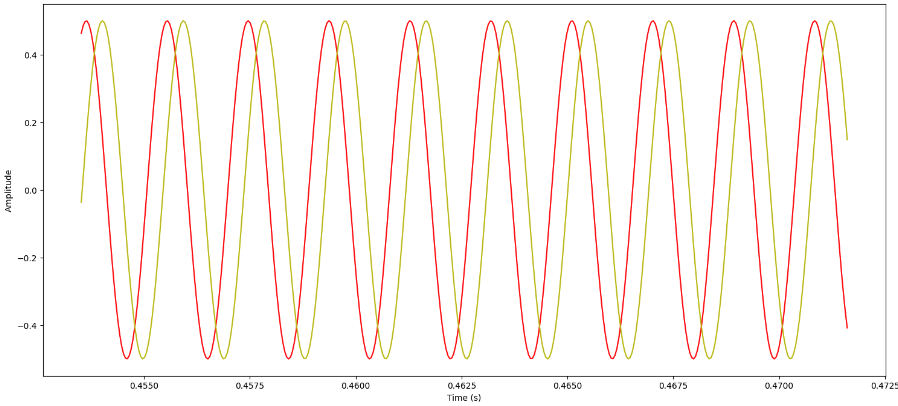

  

  Ora quello che voglio fare è mettere a confronto le sinusoide con il segnale, e aggiornare la fase trovando la sinusoide che meglio si allinea con il segnale. Nell'esempio di sotto abbiamo trovato una sinusoide che "fitta" bene il segnale, e ora ? ora per misurare la somiglianza di queste due funzioni usiamo la magnitudine, mostrata con il color senape in figura. In altre parole, per comparare le due funzioni le moltiplichiamo (sample by sample) e dopo guardiamo semplicemente all'area, aggiungendo quella positiva e sottraendo quella negativa. L'intuizione è che quando moltiplico le due funzioni e hanno lo stesso segno (quindi entrambi positive o negative), l'area sarà più positiva.

  

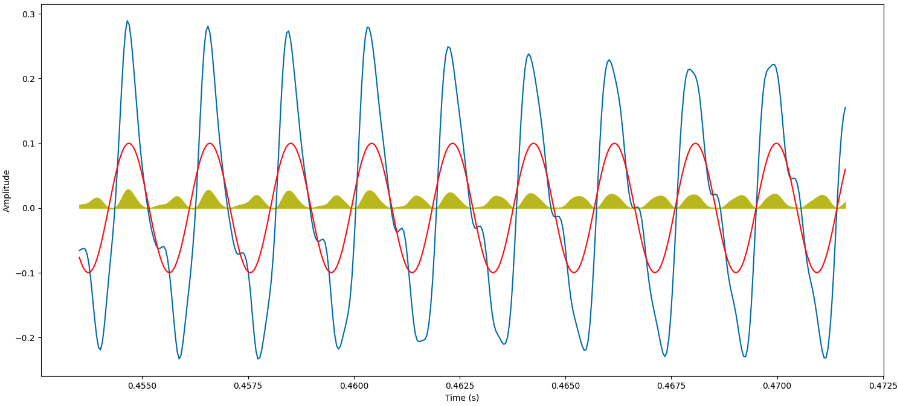
  Quindi i passi sono:

flowchart LR
Choose-frequency-->Optimise-phase
Optimise-phase-->Calculate-magnitude

• Quello che è importante da capire, è che questo è solo per una frequenza. Nella Trasformata di Fourier dobbiamo farlo per tutte le possibili frequenze. Cosi capiamo quali sono le frequenze importanti per il segnale originale. Infatti se guardiamo di nuovo lo spectrum.

• La Trasformata di Fourier a livello matematico è l'ottimizzazione della fase data una frequenza, e lo fa calcolando l'area data dalla moltiplicazione delle due funzioni tramite integrale.

• Quindi la Trasformata di Fourier viene effettuata per ogni frame.