Introduction

Nel paragrafo 2. Audio signal for Machine Learning siamo arrivati alla conversione del suono analogico in digitale. Ora il passo successivo è il Framing.

Framing

L'operazione di Framing, vuole raggruppare un insieme di samples. Come si può notare dall'immagine i frame sono in un qualche overlappati, a questo daremo una spiegazione successivamente.

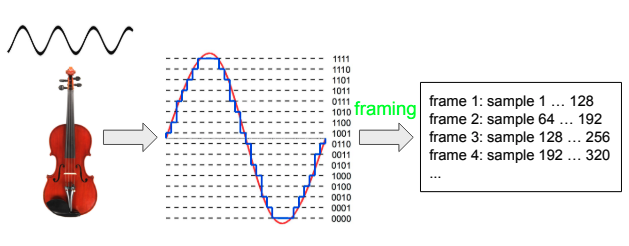
Frames

Per comprendere bene i frames, bisogna pensarli come come "pezzi di audio" che sono percettibili. Ora se noi guardiamo un singolo sample, con una sample rate di $44.1Khz$ (sampling rate della cd-rom), viene fuori che questo sample ha una durata di $0.0227ms$. Sappiamo anche che la durata di questo singolo sample è molto al di sotto della soglia alla risoluzione del suono dell'orecchio umana($10ms$). Quindi, quello che vuole fare il Framing è avere una durata sufficiente di sample per essere percettibile e apprezzabile dall'orecchio umano. Questo discorso ha senso perché quello proprietà audio che vogliamo estrarre sono in un qualche modo collegate a quello che possiamo sentire.

Un'altra caratteristica "strana" dei frames è che hanno un numero di samples alla potenza di 2. Questo perché, quando ci muoviamo nel frequency-domain, applichiamo la fast trasformata di Fourier, che è una variante e se abbiamo un numero di samples che è alla potenza di due velocizzerà di molto il processo.

I valori tipici dei frames vanno da $256$ a $8192$. E la durata del frame è data dalla seguente formula:

dove $S_r$ è la sampling rate, e $K$ la grandezza del frame.

Arrivati a questo punto, il passo successivo sarebbe quello di muoverci nel frequency domain, ma abbiamo un piccolo problema chiamato Spectral leakage.

Spectral leakage

Questo fenomeno si verifica quando nell'applicare la trasformata di Fourier a un segnale, non abbiamo un numero intero di periodi e questo succede praticamente sempre. Quello che accade è che gli endpoints di un segnale sono discontinui.

Vediamo in dettaglio perché si genera questo fenomeno: Quando si applica la DFT a un segnale finito di lunghezza 𝑁, si assume implicitamente che il segnale sia periodico con periodo 𝑁. Questo significa che il segnale si ripete all'infinito. Tuttavia, se il segnale originale non è effettivamente periodico, ci sarà una discontinuità tra l'ultimo campione e il primo campione del segmento di segnale considerato.

Il problema di avere queste discontinuità è che sono tradotte nello spectrum o nel frequency domain come componenti ad alta frequenza, ma che in realtà non esistono nell'audio.

In questa seconda immagine è possibile come queste discontinuità vengano tradotte in alte frequenze nel frequency domain.

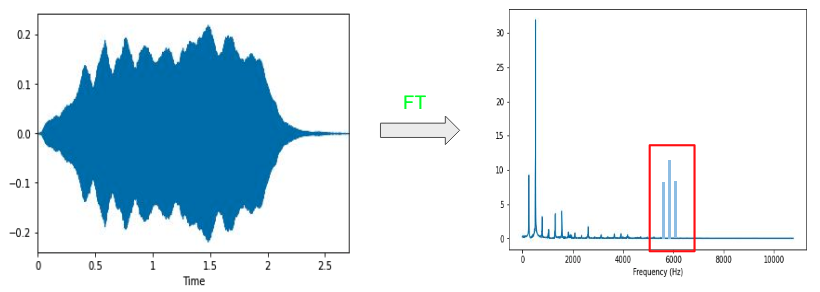
Per risolvere questo problema viene introdotta la funzione di Windowing.

Windowing

La funzione di windowing viene applicata ad ogni frame prima di passarli alla trasformata di Fourier. In questo modo eliminiamo i sample che sono alla fine degli endpoints di un frame. In altre parole, rimuoviamo completamente le informazioni dagli endpoints. Il risultato è un segnale periodico che minimizza lo spectral leakage. Nella seguente immagine abbiamo gli step e la rappresentazione del windowing. La funzione di windowing moltiplica il segnale originale con una Hann window e quello che otteniamo degli endpoints molto poco rilevanti come si vede in figura eliminando le discontinuità.

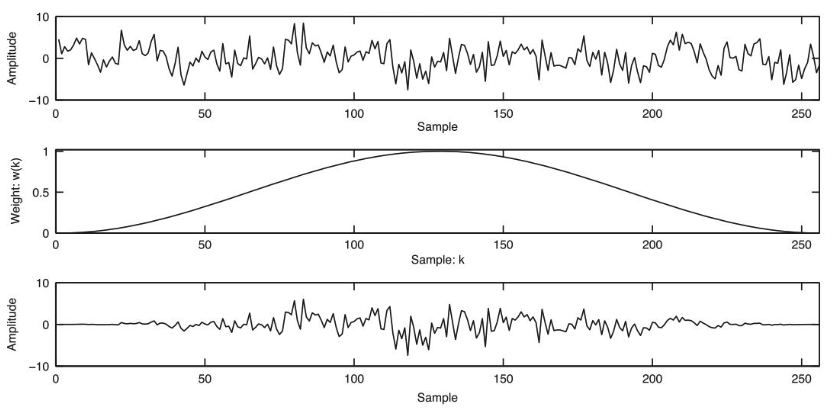
Ora abbiamo un altro grande problema, immaginate di avere più frames collegati insieme, ovviamente ci sarà una perdita di segnale nei punti di incontro.

Ma non volendo perdere segnale, possiamo ora rivelare il motivo dei frame overlappati di cui parlavamo prima nella sezione del framing.

Overlapping frames

Sovrapponendo i frames ci assicuriamo che non ci sia nessuna perdita di informazioni del segnale.

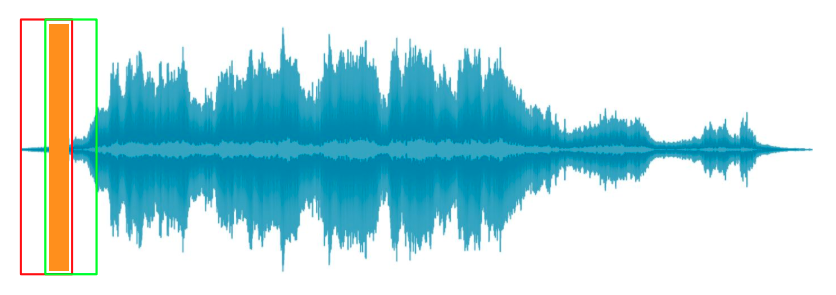
La hop length è la distanza di cui trasla a destra il frame.